After What Fraction of Period T Will the Current Again Have Its Initial Value
Inductance
96 RL Circuits
Learning Objectives
By the finish of this section, you will exist able to:
- Analyze circuits that accept an inductor and resistor in series
- Describe how current and voltage exponentially grow or disuse based on the initial conditions
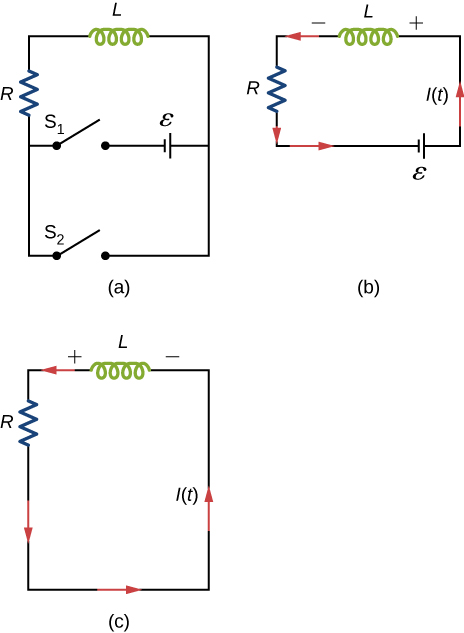
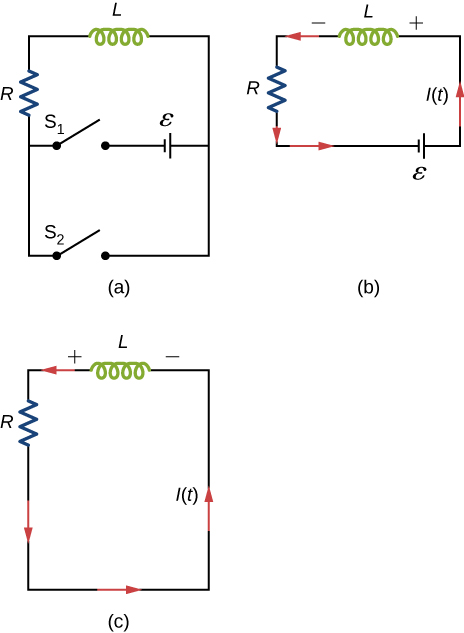
A circuit with resistance and self-inductance is known as an RL circuit. (Effigy)(a) shows an RL circuit consisting of a resistor, an inductor, a abiding source of emf, and switches ![]() and
and ![]() When
When ![]() is closed, the excursion is equivalent to a single-loop excursion consisting of a resistor and an inductor connected beyond a source of emf ((Figure)(b)). When
is closed, the excursion is equivalent to a single-loop excursion consisting of a resistor and an inductor connected beyond a source of emf ((Figure)(b)). When ![]() is opened and
is opened and ![]() is airtight, the excursion becomes a unmarried-loop circuit with but a resistor and an inductor ((Figure)(c)).
is airtight, the excursion becomes a unmarried-loop circuit with but a resistor and an inductor ((Figure)(c)).
We first consider the RL circuit of (Figure)(b). Once ![]() is closed and
is closed and ![]() is open, the source of emf produces a current in the circuit. If in that location were no self-inductance in the circuit, the electric current would rise immediately to a steady value of
is open, the source of emf produces a current in the circuit. If in that location were no self-inductance in the circuit, the electric current would rise immediately to a steady value of ![]() Nonetheless, from Faraday's law, the increasing current produces an emf
Nonetheless, from Faraday's law, the increasing current produces an emf ![]() beyond the inductor. In accordance with Lenz'southward law, the induced emf counteracts the increase in the electric current and is directed equally shown in the figure. Equally a upshot, I(t) starts at naught and increases asymptotically to its terminal value.
beyond the inductor. In accordance with Lenz'southward law, the induced emf counteracts the increase in the electric current and is directed equally shown in the figure. Equally a upshot, I(t) starts at naught and increases asymptotically to its terminal value.
Applying Kirchhoff's loop rule to this circuit, we obtain
![]()
which is a first-guild differential equation for I(t). Notice its similarity to the equation for a capacitor and resistor in series (See RC Circuits). Similarly, the solution to (Figure) can be establish by making substitutions in the equations relating the capacitor to the inductor. This gives
![]()
where
![]()
is the inductive fourth dimension constant of the circuit.
The current I(t) is plotted in (Effigy)(a). Information technology starts at zero, and as ![]() , I(t) approaches
, I(t) approaches ![]() asymptotically. The induced emf
asymptotically. The induced emf ![]() is directly proportional to dI/dt, or the slope of the curve. Hence, while at its greatest immediately after the switches are thrown, the induced emf decreases to zero with time as the current approaches its last value of
is directly proportional to dI/dt, or the slope of the curve. Hence, while at its greatest immediately after the switches are thrown, the induced emf decreases to zero with time as the current approaches its last value of ![]() The excursion then becomes equivalent to a resistor connected beyond a source of emf.
The excursion then becomes equivalent to a resistor connected beyond a source of emf.
Time variation of (a) the electric electric current and (b) the magnitude of the induced voltage across the gyre in the circuit of (Effigy)(b).
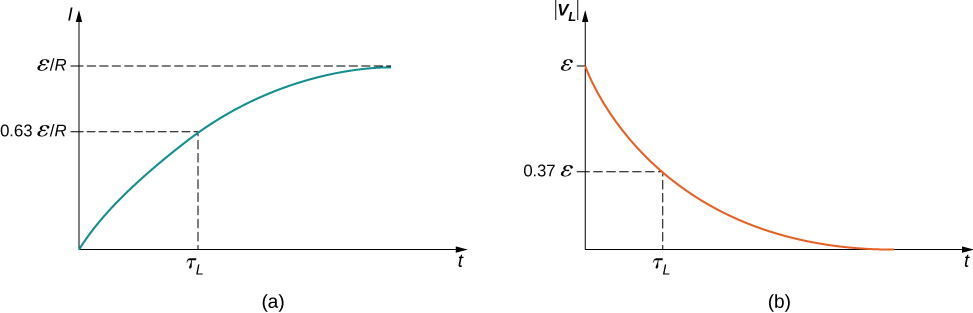
The energy stored in the magnetic field of an inductor is
![]()
Thus, as the current approaches the maximum current ![]() , the stored free energy in the inductor increases from zero and asymptotically approaches a maximum of
, the stored free energy in the inductor increases from zero and asymptotically approaches a maximum of ![]()
The fourth dimension constant ![]() tells us how chop-chop the current increases to its concluding value. At
tells us how chop-chop the current increases to its concluding value. At ![]() the current in the excursion is, from (Figure),
the current in the excursion is, from (Figure),
![]()
which is ![]() of the final value
of the final value ![]() . The smaller the inductive time constant
. The smaller the inductive time constant ![]() the more than quickly the current approaches
the more than quickly the current approaches ![]() .
.
We can detect the fourth dimension dependence of the induced voltage across the inductor in this circuit by using ![]() and (Figure):
and (Figure):
![]()
The magnitude of this role is plotted in (Effigy)(b). The greatest value of ![]() it occurs when dI/dt is greatest, which is immediately subsequently
it occurs when dI/dt is greatest, which is immediately subsequently ![]() is closed and
is closed and ![]() is opened. In the approach to steady land, dI/dt decreases to cipher. Equally a result, the voltage across the inductor besides vanishes equally
is opened. In the approach to steady land, dI/dt decreases to cipher. Equally a result, the voltage across the inductor besides vanishes equally ![]()
The time constant ![]() besides tells us how speedily the induced voltage decays. At
besides tells us how speedily the induced voltage decays. At ![]() the magnitude of the induced voltage is
the magnitude of the induced voltage is
![]()
The voltage across the inductor therefore drops to about ![]() of its initial value after once abiding. The shorter the time constant
of its initial value after once abiding. The shorter the time constant ![]() the more than rapidly the voltage decreases.
the more than rapidly the voltage decreases.
After plenty time has elapsed and so that the current has essentially reached its terminal value, the positions of the switches in (Figure)(a) are reversed, giving us the circuit in part (c). At ![]() the current in the circuit is
the current in the circuit is ![]() With Kirchhoff's loop rule, we obtain
With Kirchhoff's loop rule, we obtain
![]()
The solution to this equation is similar to the solution of the equation for a discharging capacitor, with similar substitutions. The current at time t is then
![]()
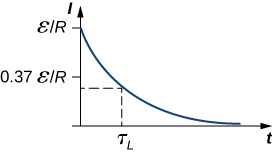
The current starts at ![]() and decreases with fourth dimension equally the free energy stored in the inductor is depleted ((Figure)).
and decreases with fourth dimension equally the free energy stored in the inductor is depleted ((Figure)).
The time dependence of the voltage beyond the inductor can be adamant from ![]()
![]()
This voltage is initially ![]() , and it decays to zero like the current. The energy stored in the magnetic field of the inductor,
, and it decays to zero like the current. The energy stored in the magnetic field of the inductor, ![]() likewise decreases exponentially with fourth dimension, as information technology is dissipated by Joule heating in the resistance of the circuit.
likewise decreases exponentially with fourth dimension, as information technology is dissipated by Joule heating in the resistance of the circuit.
Time variation of electrical electric current in the RL circuit of (Effigy)(c). The induced voltage across the gyre besides decays exponentially.
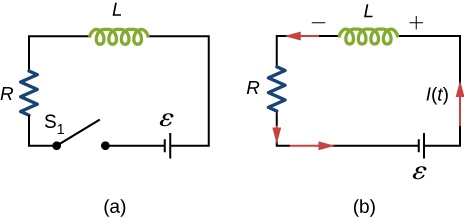
An RL Excursion with a Source of emf In the circuit of (Effigy)(a), permit ![]() With
With ![]() closed and
closed and ![]() open ((Figure)(b)), (a) what is the time constant of the circuit? (b) What are the current in the circuit and the magnitude of the induced emf beyond the inductor at
open ((Figure)(b)), (a) what is the time constant of the circuit? (b) What are the current in the circuit and the magnitude of the induced emf beyond the inductor at ![]() , and as
, and as ![]() ?
?
Strategy The fourth dimension constant for an inductor and resistor in a serial circuit is calculated using (Figure). The current through and voltage beyond the inductor are calculated by the scenarios detailed from (Figure) and (Effigy).
Solution
- The inductive time constant is
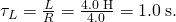
- The electric current in the circuit of (Effigy)(b) increases co-ordinate to (Effigy):
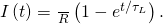
At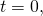
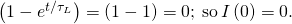
At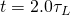 and
and 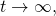 we have, respectively,
we have, respectively,
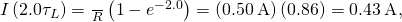
and
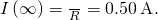
From (Figure), the magnitude of the induced emf decays as
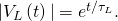
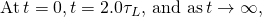 nosotros obtain
nosotros obtain
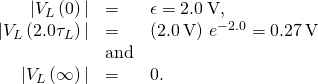
Significance If the time of the measurement were much larger than the fourth dimension abiding, we would not see the decay or growth of the voltage across the inductor or resistor. The excursion would quickly reach the asymptotic values for both of these. See (Effigy).
A generator in an RL circuit produces a square-pulse output in which the voltage oscillates between zero and some set value. These oscilloscope traces testify (a) the voltage across the source; (b) the voltage across the inductor; (c) the voltage across the resistor.
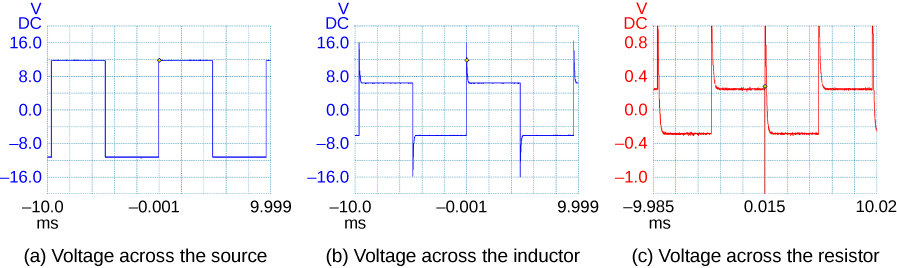
An RL Circuit without a Source of emf After the current in the RL circuit of (Figure) has reached its final value, the positions of the switches are reversed so that the excursion becomes the one shown in (Figure)(c). (a) How long does it take the current to drop to half its initial value? (b) How long does it take before the free energy stored in the inductor is reduced to ![]() of its maximum value?
of its maximum value?
Strategy The current in the inductor will at present subtract as the resistor dissipates this energy. Therefore, the current falls as an exponential decay. We can also apply that same relationship every bit a exchange for the energy in an inductor formula to notice how the energy decreases at different fourth dimension intervals.
Solution
- With the switches reversed, the current decreases co-ordinate to
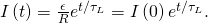
At a time t when the electric current is one-half its initial value, we accept
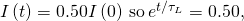
and
![Rendered by QuickLaTeX.com t=\text{−}\left[\text{ln}\left(0.50\right)\right]{\tau }_{L}=0.69\left(1.0\phantom{\rule{0.2em}{0ex}}\text{s}\right)=0.69\phantom{\rule{0.2em}{0ex}}\text{s},](https://opentextbc.ca/universityphysicsv2openstax/wp-content/ql-cache/quicklatex.com-b66955e48cb909dc28794ee3c24a3579_l3.png)
where we accept used the inductive time constant found in (Effigy). - The energy stored in the inductor is given by
![Rendered by QuickLaTeX.com {U}_{L}\left(t\right)=\frac{1}{2}L{\left[I\left(t\right)\right]}^{2}=\frac{1}{2}L{\left(\frac{\epsilon }{R}{e}^{\text{−}t\text{/}{\tau }_{L}}\right)}^{2}=\frac{L{\epsilon }^{2}}{2{R}^{2}}{e}^{-2t\text{/}{\tau }_{L}}.](https://opentextbc.ca/universityphysicsv2openstax/wp-content/ql-cache/quicklatex.com-94bb2dc0b9d7127314d09030f89f433d_l3.png)
If the energy drops to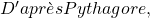 of its initial value at a time t, we have
of its initial value at a time t, we have
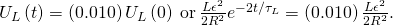
Upon canceling terms and taking the natural logarithm of both sides, we obtain
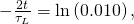
and then
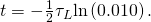
Since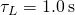 , the time it takes for the energy stored in the inductor to decrease to
, the time it takes for the energy stored in the inductor to decrease to 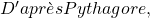 of its initial value is
of its initial value is
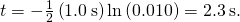
Significance This calculation only works if the circuit is at maximum current in state of affairs (b) prior to this new state of affairs. Otherwise, we start with a lower initial current, which will decay by the aforementioned relationship.
Cheque Your Understanding Verify that RC and L/R have the dimensions of time.
Check Your Agreement For the excursion of in (Effigy)(b), testify that when steady state is reached, the difference in the total energies produced by the bombardment and dissipated in the resistor is equal to the energy stored in the magnetic field of the ringlet.
Summary
Conceptual Questions
Utilise Lenz'south constabulary to explain why the initial current in the RL circuit of (Figure)(b) is zero.
As current flows through the inductor, at that place is a dorsum current by Lenz's police that is created to go on the net current at zero amps, the initial current.
When the current in the RL circuit of (Figure)(b) reaches its final value ![]() what is the voltage across the inductor? Beyond the resistor?
what is the voltage across the inductor? Beyond the resistor?
Does the time required for the current in an RL excursion to achieve any fraction of its steady-state value depend on the emf of the bombardment?
no
An inductor is continued across the terminals of a battery. Does the current that eventually flows through the inductor depend on the internal resistance of the battery? Does the fourth dimension required for the current to reach its final value depend on this resistance?
At what time is the voltage across the inductor of the RL circuit of (Figure)(b) a maximum?
At ![]() , or when the switch is first thrown.
, or when the switch is first thrown.
In the simple RL circuit of (Figure)(b), can the emf induced across the inductor ever be greater than the emf of the bombardment used to produce the current?
If the emf of the battery of (Effigy)(b) is reduced by a gene of ii, by how much does the steady-state energy stored in the magnetic field of the inductor change?
one/4
A steady current flows through a circuit with a big inductive time abiding. When a switch in the circuit is opened, a large spark occurs across the terminals of the switch. Explain.
Draw how the currents through ![]() shown below vary with time after switch S is closed.
shown below vary with time after switch S is closed.
Initially, ![]() and
and ![]() , and after a long time has passed,
, and after a long time has passed, ![]() and
and ![]() .
.
Talk over possible practical applications of RL circuits.
Problems
a. four.0 A; b. 2.4 A; c. on R: ![]() ; on Fifty:
; on Fifty: ![]()
The current in the RL circuit shown here increases to  of its steady-state value in 2.0 s. What is the time constant of the circuit?
of its steady-state value in 2.0 s. What is the time constant of the circuit?
How long after switch ![]() is thrown does it accept the current in the circuit shown to achieve half its maximum value? Express your answer in terms of the time abiding of the circuit.
is thrown does it accept the current in the circuit shown to achieve half its maximum value? Express your answer in terms of the time abiding of the circuit.
![]()
Examine the circuit shown beneath in part (a). Make up one's mind dI/dt at the instant afterward the switch is thrown in the circuit of (a), thereby producing the circuit of (b). Show that if I were to continue to increase at this initial rate, information technology would reach its maximum ![]() in one fourth dimension abiding.
in one fourth dimension abiding.
The current in the RL circuit shown below reaches half its maximum value in 1.75 ms afterwards the switch ![]() is thrown. Decide (a) the time constant of the circuit and (b) the resistance of the excursion if
is thrown. Decide (a) the time constant of the circuit and (b) the resistance of the excursion if ![]() .
.
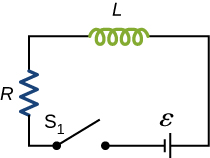
a. 2.52 ms; b. ![]()
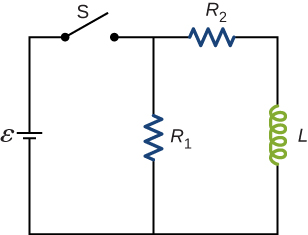
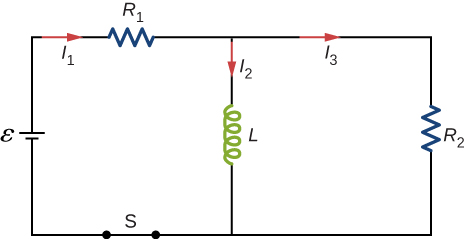
Consider the excursion shown beneath. Find ![]() when (a) the switch S is first closed, (b) afterward the currents have reached steady-state values, and (c) at the instant the switch is reopened (later on beingness closed for a long fourth dimension).
when (a) the switch S is first closed, (b) afterward the currents have reached steady-state values, and (c) at the instant the switch is reopened (later on beingness closed for a long fourth dimension).
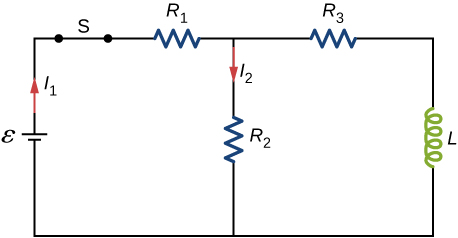
For the excursion shown beneath, observe the current through the inductor ![]() later on the switch is reopened.
later on the switch is reopened.
Show that for the circuit shown beneath, the initial energy stored in the inductor, ![]() , is equal to the total energy somewhen dissipated in the resistor,
, is equal to the total energy somewhen dissipated in the resistor, ![]() .
.
proof
Glossary
- inductive time constant
- denoted past
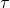 , the feature time given by quantity L/R of a particular serial RL circuit
, the feature time given by quantity L/R of a particular serial RL circuit
Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/rl-circuits/
0 Response to "After What Fraction of Period T Will the Current Again Have Its Initial Value"
Post a Comment